k-Nearest Neighbour

K-Nearest Neighbour or KNN for short is a supervised machine learning algorithm that can be used for both classification and regression tasks. KNN is a non-parametric model, meaning that it does not need to learn any parameters. For each target the model looks up the k nearest neighbours in the dataset and bases its prediction on the values of those points.

The Algorithm - Classification

1. Choose hyperparameter k, which determines how many neighbours are taken into account for the prediction.
2. Calculate the distance between the target datapoint and all datapoints in the dataset.
3. Order the datapoints by distance to the target and select the k closest points.
4. Count the number of occurrences per class.
5. The majority class is assigned to the target as prediction.

The Algorithm - regression

4. Take the average of the k closest points as prediction.

The most common measure for finding the distances is the Euclidean distance:

Implementation

Let’s implement a simple version of the KNN algorithm for both the classification and the regression task. We assume that the data is multi-dimensional and that the target variable for classification is an integer, and a float for regression. The data is as follows:

We will set up a class KNN and add the functions along the way. When initialising the class we give two parameters; k and objective. k is the hyperparameter that determines the number of neighbours that are taken into account and the objective indicates if it is a classification or regression problem.

class KNN:
    def __init__(self, k: int, objective: str):
        self.k = k
        self.objective = objective

        self.x = None
        self.y = None

First we want to store the data in the class, therefore we need a train function that does this.

def train(self, x, y):
    self.x = x
    self.y = y

We would also like a function that calculates the euclidean distance between two points. For the purpose of this tutorial we will do it in pure python, but it is also possible to do it with numpy.

import math

def euclidean_distance(self, p, q):
    distance = 0
    for p_i, q_i in zip(p, q):
        distance += (p_i - q_i) ** 2
    return math.sqrt(distance)

The next step is to calculate the distances between all points in the dataset and find the k closest points. We will take care of this in the predict function:

from collections import Counter

def predict(self, x):
    distances = [
        (
            self.euclidean_distance(x, x_i),
            y_i,
        )
        for x_i, y_i in zip(self.x, self.y)
    ]
    
    k_closest = sorted(distances)[:self.k]
    labels = [label for dist, label in k_closest]
    
    if self.objective == "classification":
        return Counter(labels).most_common()[0][0]
    elif self.objective == "regression":
        return sum(labels) / len(labels)

Choosing a value for k

The hyperparameter k is a chosen parameter and thus needs to be tuned in order to find the best model (i.e. model with the highest test accuracy). This is done by performing multiple runs of the model with a varying value for k. The ideal is chosen by picking the model that performs best on unseen data (the test set).

After splitting the dataset in a train and test and running iteration for various values of k, the results are shown in the plot below:

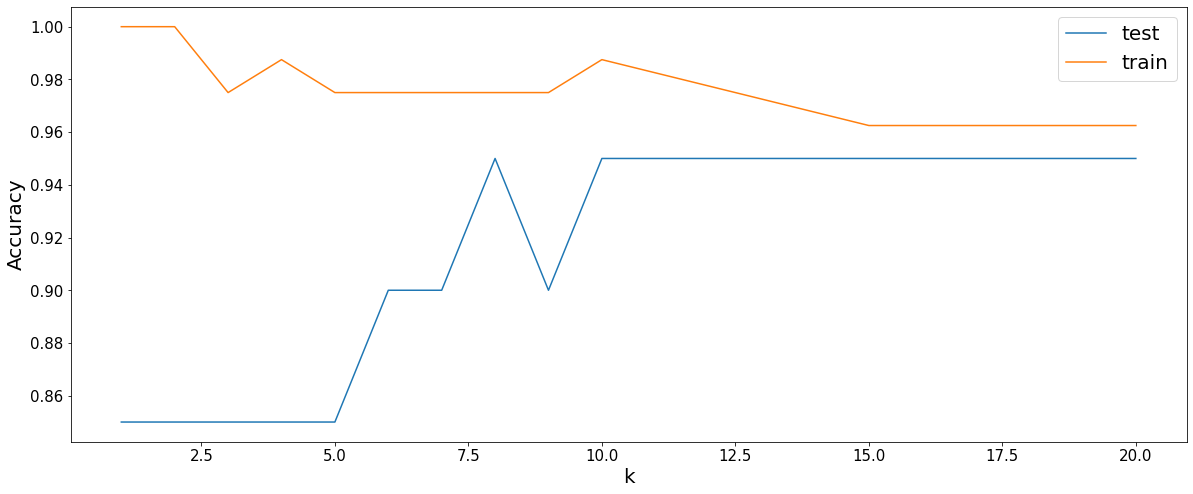
From the plot we can see that a low value for k yields a high train accuracy (of a 100%), but a low test accuracy. This is also known as overfitting, where the model is fitted perfectly on the train data but lacks the generalisation to unseen data. When the value of k is increases a more generalised model is found where performance on the train and test data are close to each other.

Below another plot is showing the decision boundary for various values for k. If we compare the plot for and we can clearly see the difference in generalisation, where for the model is overfitting to each data point.

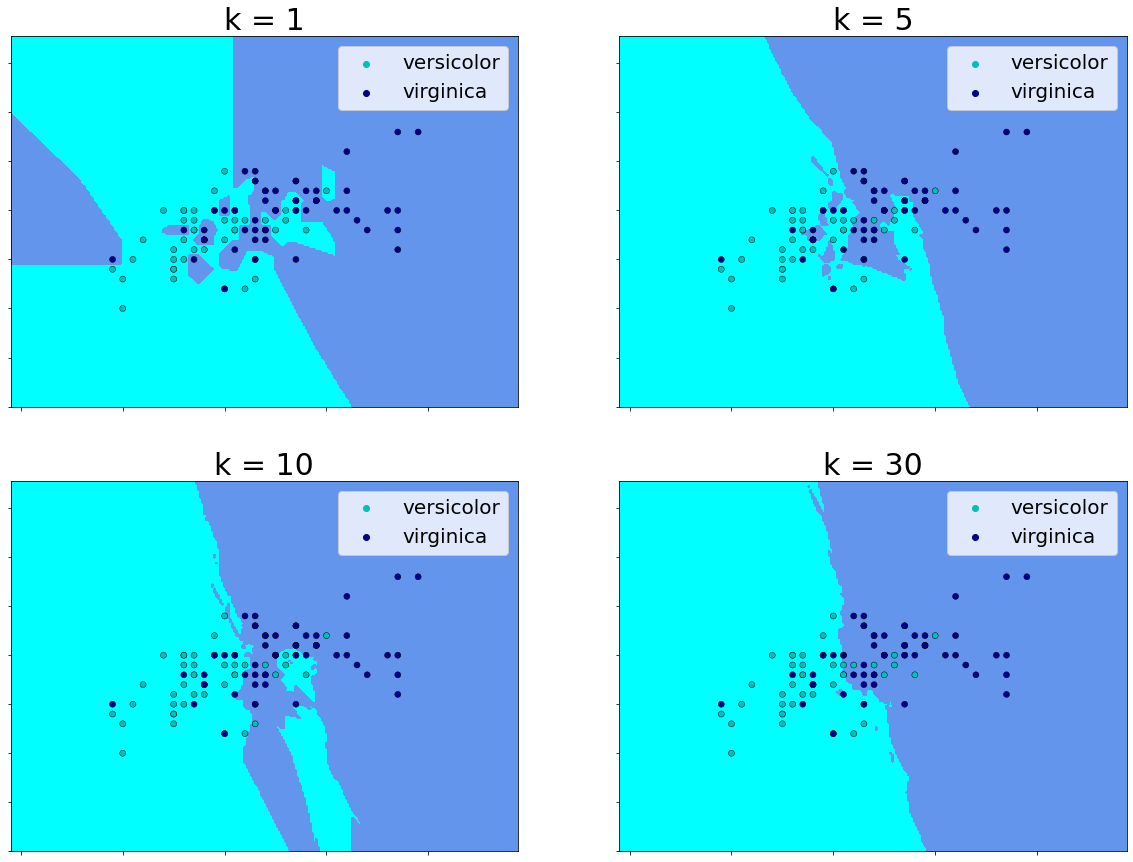
Pros and Cons

Pros of KNN:

• Simple, only need to tune one parameter.
• Applicable to multi-class problems.
• Good performance, effective in low dimensional data.

Cons of KNN:

• Costly to compute distances to all points in search for closest neighbour(s).
• Memory limitation, must store all data-points in the dataset. This will cause problems when the dataset becomes too big.

Complete code

The notebook with the code can be found here on GitHub. Here is the complete class for the KNN model:

import math
from collections import Counter

class KNN:
    def __init__(self, k: int, objective: str):
        self.k = k
        self.objective = objective

        self.x = None
        self.y = None

    def train(self, x, y):
        self.x = x
        self.y = y
    

    def euclidean_distance(self, p, q):
        distance = 0
        for p_i, q_i in zip(p, q):
            distance += (p_i - q_i) ** 2
        return math.sqrt(distance)
    

    def predict(self, x):
        distances = [
            (
                self.euclidean_distance(x, x_i),
                y_i,
            )
            for x_i, y_i in zip(self.x, self.y)
        ]

        k_closest = sorted(distances)[:self.k]
        labels = [label for dist, label in k_closest]
        
        if self.objective == "classification":
            return Counter(labels).most_common()[0][0]
        elif self.objective == "regression":
            return sum(labels) / len(labels)